안녕하세요.
Splay Tree의 활용 중 가장 많이 사용되는 구간 쿼리에 대해 알아보겠습니다.
Kth 원소 찾기
Tree 상에서 k번째 원소가 무엇인지 찾는 연산입니다.
구간 쿼리를 하려면 kth 원소가 무엇인지 알아야 합니다.
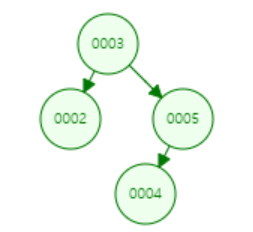
- first element : 2
- second element : 3
- 4th element : 5
가장 쉽게 구하는 방식으로는, 중위 순회해서 원소들의 리스트를 다 뽑아줍니다.
그리고 그 중 kth 원소를 인덱스를 통해 접근하면 됩니다.
하지만 이 방식은 O(N)의 시간 복잡도가 걸립니다.
스플레이 트리는 이를 다른 방식으로 찾아 O(log N) 만에 가능합니다.
Node 구조체
자신을 루트로 하는 서브트리의 크기를 알아야 합니다.
이를 childCnt로 Node 구조체 안에 변수로 선언했습니다.
rotate할 때 자식과 부모의 위치가 바뀝니다.
기존의 부모 노드를 update 한 후 자신 노드를 update 합니다.
struct Node {
Node* left;
Node* right;
Node* parent;
int key;
int childCnt;
Node(ll k) {
...
childCnt = 1;
}
...
int getChild() { return childCnt; }
void update() {
childCnt = 1;
if (left) childCnt += left->childCnt;
if (right) childCnt += right->childCnt;
}
void rotate() {
...
p->update();
update();
}
};get_kth
현재 서브트리에서 몇 번째에 위치하는지를 currentCnt 변수로 나타냈습니다.
currentCnt가 k랑 같다면 => 현재 위치를 splay 하고 끝
currentCnt < k => 오른쪽 서브트리로 이동
currentCnt > k => 왼쪽 서브트리로 이동
struct SplayTree {
...
void findKth(int k) {
Node* x = root;
while (x) {
int currentCnt = (x->left ? x->left->getChild() : 0) + 1;
if (currentCnt == k) {
splay(x);
break;
}
if (currentCnt < k) {
x = x->right;
k -= currentCnt;
}
else x = x->left;
}
}
int getKth(int k) {
findKth(k);
return root->key;
}
};구간 합 구하기
위에서 구한 findKth 함수를 활용해 구간 합을 O(log N)에 구할 수 있습니다.
Node 구조체
sum : 자신을 포함한 서브트리의 구간 합
key : 자신 노드의 key 값
update 할 때 sum도 바꿔줍니다.
struct Node {
Node* left;
Node* right;
Node* parent;
ll key, sum;
int childCnt;
Node(ll k) {
left = right = parent = NULL;
sum = key = k;
childCnt = 1;
}
void update() {
childCnt = 1;
sum = key;
if (left) {
childCnt += left->childCnt;
sum += left->sum;
}
if (right) {
childCnt += right->childCnt;
sum += right->sum;
}
}
...
};BST의 특성이 사라짐
구간 쿼리를 처리하기 위해선 BST의 특성을 버려야 합니다.
BST는 모든 서브트리에서 아래 특성을 가집니다.
- 왼쪽 모든 서브트리의 key < 루트 노드의 key
- 루트 노드의 key < 오른쪽 모든 서브트리의 key
이를 key 값이 아닌, 인덱스를 기준으로 BST를 구성해야 합니다.
인덱스가 작을수록 => 트리에서 왼쪽에 위치하게 합니다.
init 함수를 보면, 제일 왼쪽과 제일 오른쪽 노드를 Dummy Node로 만들어줍니다.
=> 구간을 뽑을 때 nullptr을 마주하지 않기 위함입니다.
(이에 대한 설명은 아래에 '특정 구간 [L, R] 추출하기'에서 설명이 되어있습니다.)
struct SplayTree {
Node* root;
void init(int N) {
root = new Node(-1);
while (N--) {
ll key;
scanf("%lld", &key);
merge(key);
}
merge(-1);
}
void merge(ll key) {
Node* x = new Node(key);
root->parent = x;
x->left = root;
splay(root);
}
...
};특정 인덱스의 key 값 변경
세그먼트 트리에서 이걸 O(log N) 만에 update가 가능했습니다.
스플레이 트리도 마찬가지로 O(log N) 만에 가능합니다.
idx에 해당하는 노드를 findKth 함수를 통해 루트로 올려줍니다.
루트의 key 값을 변경하고 update 해주면 됩니다.
struct SplayTree {
...
void update(int idx, ll v) {
findKth(idx);
root->key = v;
root->update();
}
};특정 구간 [L, R] 추출하기
임의의 구간 [L, R]을 O(log N) 만에 뽑아낼 수 있습니다.
아래와 같이 트리를 구성하면
root->right->left가 구간 [L, R]이 됩니다.

왼쪽 끝과 오른쪽 끝에 Dummy Node를 둔 이유는
L-1이나 R+1이 nullPtr이 되는 것을 방지하기 위함입니다.
구간 [L, R]에 접근하려면 root->right->left로 접근해야 하는데 둘 중 하나라도 nullptr이 되면 접근이 불가능하기 때문입니다.
R+1에 해당하는 노드를 루트로 올려줍니다.
그리고 tmp에 해당 노드를 저장합니다.
L-1에 해당하는 노드를 루트로 올려줍니다.
tmp를 루트의 자식이 될 때 까지 올려줍니다.
struct SplayTree {
Node* root;
...
void splay(Node* x, Node* y = NULL) {
while (x->parent != y) {
Node* p = x->parent;
if (p->parent != y) {
if (p->isLeft() == x->isLeft()) p->rotate();
else x->rotate();
}
x->rotate();
}
if (!y) root = x;
}
ll getSum(int l, int r) {
findKth(r + 1);
Node* tmp = root;
findKth(l - 1);
splay(tmp, root);
return root->right->left->sum;
}
};문제
https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
참고 자료
https://cubelover.tistory.com/10
Splay Tree
Splay Tree는 Binary Search Tree의 한 종류이다. 삽입, 삭제, 검색 등의 쿼리를 amortized O(log n)에 처리 가능하며 Splay 연산을 이용해서 구간에 대한 쿼리가 자유롭고 AVL Tree나 Red-Black Tree와 같은 다른 Binary
cubelover.tistory.com
'알고리즘 & 자료구조' 카테고리의 다른 글
| Splay Tree (4) - Lazy Propagation, 구간 뒤집기 (0) | 2023.11.05 |
|---|---|
| Splay Tree (2) - find, insert, delete, 최솟값 최댓값 찾기 (2) | 2023.10.02 |
| Splay Tree (1) - rotate, splay (1) | 2023.09.26 |
| 곱셈의 역원 (0) | 2023.09.18 |
| 확장 유클리드 알고리즘 (0) | 2023.09.18 |


