안녕하세요.
LIS (Longest Increasing Sequence)에 대해 알아보겠습니다.
개념
LIS는 최장 증가 부분 수열이라고 합니다.
수열에서 가장 긴 증가하는 부분 수열입니다.

arr에서 가장 긴 부분 수열은 {2, 4, 8, 9} 입니다.
이를 LIS라고 말하고 LIS의 길이는 4 입니다.
(부분 수열은 연속하지 않아도 됨)
풀이
LIS를 구하는 여러 방법 중에서 아래 2가지 방법을 알아보겠습니다.
- DP 사용
- 이분 탐색 사용
DP 사용
과정
dp[i]를 arr[i]를 마지막 원소로 갖는 LIS의 길이 라고 둔다면,
0 <= j < i && arr[j] < arr[i] 를 만족할 때 dp[i] = max { dp[j] + 1 } 입니다.
0 <= i < N에 대해 max { dp[i] } 가 LIS 길이입니다.

0 <= j < 0 중에서 arr[j] < arr[0]을 만족하는 경우는 없습니다.
그래서 자기 자신만 포함하는 길이인 1을 dp[0]에 넣어줍니다.

0 <= j < 1 중에서 arr[j] < arr[1]을 만족하는 경우는 없습니다.
dp[1] = 1을 넣어줍니다.

0 <= j < 2 중에서 arr[j] < arr[2]를 만족하는 경우가 있습니다.
- arr[1] < arr[2] : dp[1] + 1 = 2
만족하는 경우 중 가장 최댓값인 2를 dp[2]에 넣어줍니다.
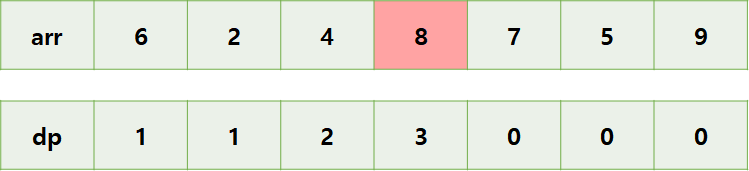
0 <= j < 3 중에서 arr[j] < arr[3]를 만족하는 경우가 있습니다.
- arr[0] < arr[3] : dp[0] + 1 = 2
- arr[1] < arr[3] : dp[1] + 1 = 2
- arr[2] < arr[3] : dp[2] + 1 = 3
이 중 최댓값이 3이므로 dp[3] = 3을 해줍니다.

0 <= j < 4 중에서 arr[j] < arr[4]를 만족하는 경우가 있습니다.
- arr[0] < arr[4] : dp[0] + 1 = 2
- arr[1] < arr[4] : dp[1] + 1 = 2
- arr[2] < arr[4] : dp[2] + 1 = 3
dp[4] = 3을 해줍니다.

0 <= j < 5 중에서 arr[j] < arr[5]를 만족하는 경우가 있습니다.
- arr[1] < arr[5] : dp[1] + 1 = 2
- arr[2] < arr[5] : dp[2] + 1 = 3
dp[5] = 3

0 <= j < 6 중에서 arr[j] < arr[6]를 만족하는 경우
- arr[0] < arr[6] : dp[0] + 1 = 2
- arr[1] < arr[6] : dp[1] + 1 = 2
- arr[2] < arr[6] : dp[2] + 1 = 3
- arr[3] < arr[6] : dp[3] + 1 = 4
- arr[4] < arr[6] : dp[4] + 1 = 4
- arr[5] < arr[6] : dp[5] + 1 = 4
dp[6] = 4
LIS의 길이는 dp[i] (0 <= i < N) 중 가장 큰 값입니다.
=> 4
시간 복잡도
dp[i]의 값을 계산하기 위해 0 <= j < i 의 값을 확인했습니다.
1 + 2 + ... + N-1개를 보며 이는 (N-1) * (N) / 2 입니다.
=> O(N * N)
코드
문제 - 기본 문제 1의 코드
다이나믹 프로그래밍을 이용한 코드입니다.
#include <cstdio>
const int SIZE = 1004;
int arr[SIZE];
inline int max(int a, int b) { return a > b ? a : b; }
struct LIS {
int dp[SIZE];
int solve(int N) {
int ret = 0;
for (int i = 0; i < N; ++i) {
dp[i] = 1;
for (int j = 0; j < i; ++j) {
if(arr[j] < arr[i])
dp[i] = max(dp[i], dp[j] + 1);
}
ret = max(ret, dp[i]);
}
return ret;
}
}lis;
int main()
{
//freopen("input.txt", "r", stdin);
int N;
scanf("%d", &N);
for (int i = 0; i < N; ++i) scanf("%d", &arr[i]);
printf("%d\n", lis.solve(N));
}이분 탐색 사용
O(N * N) 시간 복잡도는 문제에 따라 오래 걸리는 경우가 있습니다.
이보다 더 빠르게 LIS를 구하는 방법을 알아보겠습니다.
과정
기존의 입력 값을 담은 arr 배열 말고, lis 배열을 하나 더 준비합니다.
(lis 배열 : j < i 에 대해 arr[j] < arr[i]를 만족하는 배열)
arr[i]가 lis 배열에서 어디에 들어가는지를 이분 탐색으로 찾습니다.
찾는 위치는 arr[i]보다 크거나 같은 원소 중 가장 작은 원소의 위치 입니다.
(lower_bound와 같은 의미 입니다.)

6이 lis에 어디에 들어가는지 찾아줍니다.
처음, lis는 빈 배열이므로 lis에 6보다 크거나 같은 원소는 없습니다.
그래서 lis 첫 번째 위치에 6을 넣어줍니다.

2보다 크거나 같은 lis의 원소 중 가장 작은 값은 6 입니다.
6이 있는 자리에 2를 갱신해줍니다.
이미 원소가 들어있는 자리에 값을 넣을 때는 더 작은 값을 넣어줍니다.
(이에 대한 이유는 과정을 하나만 더 보고 설명하겠습니다.)

lis 배열에 4보다 크거나 같은 원소는 없으므로 끝에 붙여줍니다.
아까 단계에서 lis 첫 번째 위치에 2가 아닌 6을 넣었다면,
4보다 크거나 같은 원소를 찾으면 6이 나옵니다.
현재까지 lis는 {2, 4} 인데 잘못된 lis인 {6}이 나옵니다.
그래서 위치가 겹칠 때는 더 작은 값을 갱신해줍니다.

arr의 모든 원소를 위와 같은 과정을 거치면 위 그림처럼 나옵니다.
이렇게 마지막 단계까지 다가와서 lis에 담긴 원소의 개수를 구하면 됩니다.
=> 4
시간 복잡도
lower_bound 위치를 찾는데 O(log N)이 걸립니다.
이를 N번 반복하니 최종 시간 복잡도는
O(N * logN) 이 나옵니다.
코드
문제 - 기본 문제2의 코드입니다.
#include <cstdio>
const int SIZE = 1e6 + 4;
int arr[SIZE];
inline int min(int a, int b) { return a < b ? a : b; }
struct Vector {
int arr[SIZE];
int sz;
inline void push(int n) { arr[sz++] = n; }
void put(int idx, int n) {
if (idx == sz) push(n);
else arr[idx] = min(arr[idx], n);
}
inline int operator[](int idx) { return arr[idx]; }
}vec;
int lower(int key) {
int l = 0, r = vec.sz - 1;
while (l <= r) {
int m = l + r >> 1;
if (key <= vec[m]) r = m - 1;
else l = m + 1;
}
return r + 1;
}
struct LIS {
int solve(int N) {
for (register int i = 0; i < N; ++i) {
int t = lower(arr[i]);
vec.put(t, arr[i]);
}
return vec.sz;
}
}lis;
int main()
{
//freopen("input.txt", "r", stdin);
int N;
scanf("%d", &N);
for (int i = 0; i < N; ++i) scanf("%d", &arr[i]);
printf("%d\n", lis.solve(N));
}실제 LIS 추출하기
지금까지 알아본 알고리즘은 lis의 길이를 구하기 위한 알고리즘 입니다.
실제 lis를 추출하기 위해선 추가 과정이 필요합니다.
잘못된 과정

아까 봤던 case는 운이 좋게도 lis 배열에 담긴 원소들의 순서가
arr에서 lis를 찾는 것과 같은 결과를 가져옵니다.

이 case를 다시 탐색해보겠습니다.


길이는 2가 맞지만,
lis 배열에 담긴 대로 arr 배열을 확인해보니 lis가 아닙니다.
과정
lis 배열에 들어가는 위치를 따로 저장해놓을 idx 배열이 필요합니다.
idx 배열을 뒤에서부터 탐색하면서 lis.size, lis.size-1, lis.size-2, ... , 1, 0 이 처음으로 나오는 위치를 역으로 출력하면 됩니다.

첫 번째 원소는 lis의 첫 번째 자리에 들어갑니다.
idx[0] = 0 으로 갱신해줍니다.

두 번째 원소 역시 lis의 첫 번째 자리에 들어갑니다.
idx[1] = 0

4는 lis에서 두 번째 자리에 들어갑니다.
idx[2] = 1

1은 lis의 첫 번째 자리에 위치합니다.
idx[3] = 0 으로 갱신해줍니다.

idx 배열을 뒤에서 부터 탐색합니다.
현재 lis 길이는 2이고,
idx 배열에서 처음으로 1, 0을 만나는 원소가 lis에 포함됩니다.
처음으로 1을 만나는 원소 => 4
처음으로 0을 만나는 원소 => 2
=> lis = {2, 4} 가 됩니다.
코드
문제 - 기본 문제 3의 코
#include <cstdio>
const int SIZE = 1e6 + 4;
int arr[SIZE];
inline int min(int a, int b) { return a < b ? a : b; }
struct Vector {
int arr[SIZE];
int sz;
inline void push(int n) { arr[sz++] = n; }
void put(int idx, int n) {
if (idx == sz) push(n);
else arr[idx] = min(arr[idx], n);
}
inline int operator[](int idx) { return arr[idx]; }
}vec;
int lower(int key) {
int l = 0, r = vec.sz - 1;
while (l <= r) {
int m = l + r >> 1;
if (key <= vec[m]) r = m - 1;
else l = m + 1;
}
return r + 1;
}
struct LIS {
int idx[SIZE];
Vector lis;
void trace(int N) {
int cur = vec.sz - 1; // the length of LIS
register int i;
for (i = N - 1; i >= 0; --i) {
if (idx[i] == cur) {
lis.push(arr[i]);
--cur;
}
}
for (i = lis.sz - 1; i >= 0; --i)
printf("%d ", lis[i]);
}
void solve(int N) {
for (register int i = 0; i < N; ++i) {
int t = idx[i] = lower(arr[i]);
vec.put(t, arr[i]);
}
printf("%d\n", vec.sz);
trace(N);
}
}lis;
int main()
{
//freopen("input.txt", "r", stdin);
int N;
scanf("%d", &N);
for (int i = 0; i < N; ++i) scanf("%d", &arr[i]);
lis.solve(N);
}문제
기본 문제 1 : https://www.acmicpc.net/problem/11053
11053번: 가장 긴 증가하는 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
기본 문제 2 : https://www.acmicpc.net/problem/12015
12015번: 가장 긴 증가하는 부분 수열 2
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000,000)
www.acmicpc.net
기본 문제 3 : https://www.acmicpc.net/problem/14003
14003번: 가장 긴 증가하는 부분 수열 5
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (-1,000,000,000 ≤ Ai ≤ 1,000,000,000)
www.acmicpc.net
응용 문제 1 : https://www.acmicpc.net/problem/23035
23035번: 가톨릭대는 고양이를 사랑해
첫 번째 줄에 정수 N, M(0 ≤ N, M ≤ 1,000,000,000)이 주어진다. 두 번째 줄에 고양이의 수를 나타내는 정수 T(0 ≤ T ≤ 100,000)가 주어진다. 세 번째 줄부터 T개의 줄에 고양이의 위치를 나타내는 정수 r,
www.acmicpc.net
응용 문제 2 : https://www.acmicpc.net/problem/13711
13711번: LCS 4
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, [1, 2, 3]과 [1, 3, 2]의 LCS는 [1, 2] 또는 [1, 3]
www.acmicpc.net
참고 자료
LIS (Longest Increasing Subsequence) - 최장 증가 부분 수열
주어진 수열에서 을 구하는 문제 유형을 알아보자. 사실 이 유형은 DP(Dynamic Programming) 문제로 자주 나오는 유형이며, O(N^2)의 시간복잡도를 갖는 알고리즘과 O(NlogN)의 시간 복잡도를 갖는 알고리
rebro.kr
'알고리즘 & 자료구조' 카테고리의 다른 글
| Rabin Karp (라빈 카프) 알고리즘 (0) | 2023.09.12 |
|---|---|
| 냅색 (Knapsack) (0) | 2023.08.13 |
| 2-SAT (0) | 2023.07.24 |
| 강한 연결 요소 (Strongly Connected Component) (0) | 2023.07.20 |
| 최소 스패닝 트리 (Minimun Spanning Tree) (0) | 2023.07.14 |



