안녕하세요.
오늘은 최소 스패닝 트리에 대해 알아보겠습니다.
스패닝 트리 중 가장 가중치가 작은 트리
스패닝 트리가 무엇인지 먼저 알아야합니다.
그래프
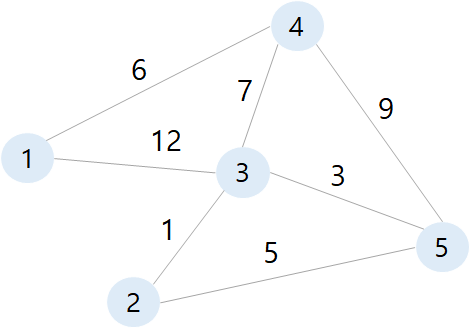
그래프는 위 그림과 같이 노드와 간선으로 구성되는 자료구조입니다.
트리
그래프 그림을 보면 사이클이 존재합니다.
사이클이란, 어떤 노드에서 출발해서 간선을 최대 1번만 이용해서 자신 노드로 돌아오는 것을 말합니다.
(3 - 4 - 5 - 3, 3 - 2 - 5 - 3 등)
트리는 사이클이 없는 acyclic graph 라고 합니다.
스패닝 트리

관련 유투브 영상을 찾아봤는데 영어로 아래와 같이 설명합니다.
hit all vertices of graph G
그래프의 모든 노드에 도달하는 트리라는 뜻입니다.
트리이기 때문에 사이클이 없는 것을 확인할 수 있습니다.
최소 스패닝 트리

하나의 그래프에서 여러 스패닝 트리가 나올 수 있습니다.
최소 스패닝 트리는 이 중에서 가장 비용이 작은 스패닝 트리를 말합니다.
(스패닝 트리 비용은 남겨져있는 간선의 비용 합으로 계산합니다)
알고리즘
최소 스패닝 트리를 구하는 방법에는 2가지가 있습니다.
- 크루스칼 알고리즘
- 프림 알고리즘
2가지 방법을 다 알아보겠습니다.
크루스칼 알고리즘 (Kruskal Algorithm)
작동 과정
- 비용을 기준으로 간선을 오름차순 정렬
- 오름차순 순서로 간선을 하나씩 확인하면서 아래 과정을 반복
- 정점 (u, v) 가 이미 같은 트리에 존재하면 => continue
- 정점 (u, v)가 다른 트리에 존재하면 => 최소 신장 트리에 포함시킴
- 최소 신장 트리에 포함된 정점이 N개가 되면 종료
그림과 같이 자세히 알아보겠습니다.

먼저, 비용을 기준으로 간선을 오름차순 합니다.
오른쪽 표가 간선을 오름차순으로 정리한 것입니다.

첫 간선 (2, 3, 1) 을 확인합니다.
2번과 3번 정점은 각각 다른 subtree에 속하므로 두 정점을 합칩니다.
cost : 0 + 1 = 1

3번과 5번 정점 역시 각각 다른 subtree에 속하므로 두 정점을 합칩니다.
cost : 1 + 3 = 4

2번과 5번 정점은 다른 subtree에 속하므로 간선을 포함시키지 않습니다.
간선을 포함시키지 않았으므로 cost는 그대로 4입니다.
cost : 4 + 0 = 4

1번과 4번 정점은 다른 subtree에 속하므로 두 정점을 합칩니다.
cost : 4 + 6 = 10

3번과 4번 정점은 다른 subtree에 속하므로 두 정점을 합칩니다.
cost : 10 + 7 = 17

모든 정점이 하나의 subtree에 포함되었으므로 종료합니다.
그래프 G의 최소 스패닝 트리의 비용은 17 입니다.
시간 복잡도
간선을 오름차순으로 정렬하면 O(E logE) 가 됩니다. (E : 간선의 개수)
정점 사이클 확인은 유니온 파인드를 사용하면 됩니다. O(1)
=> O(E logE)
증명
크루스칼 알고리즘은 매 순간 비용이 짧은 간선을 확인하기 때문에 그리디 알고리즘의 일종입니다.
그리디의 증명 방법을 사용해서 크루스칼 알고리즘을 증명할 수 있습니다.
(귀류법을 통한 증명)
귀류법
- 가정 : 크루스칼 알고리즘으로 선택된 간선 e1이 최소 스패닝 트리 T에 포함되지 않는다
위 가정에 들어맞는 간선 e1이 (u, v, cost) 라고 두겠습니다.
(u, v : 간선이 연결하는 두 정점 // cost : 간선의 비용)
최소 스패닝 트리 T 상에서는 u와 v를 e1을 사용하지 않고 다른 경로로 연결이 되어 있습니다.

이 경로에 포함된 간선 중 적어도 하나는 cost 보다 크거나 같은 비용을 가진 간선이 존재합니다.
- 그렇지 않다면 (모두 작다면), 해당 경로를 구성하는 간선들이 크루스칼 알고리즘에 의해 이전에 모두 선택됩니다.
- u와 v를 연결하는 경로가 존재한다는 모순에 빠집니다.
그럼 경로 상의 간선들 중 cost 보다 크거나 같은 가중치를 가진 간선을 없애고 e1을 택하면 최소 스패닝 트리 T의 가중치는 줄거나 같아집니다.
즉, 크루스칼 알고리즘으로 선택한 간선으로 대체해도 손해보지 않기 때문에 크루스칼 알고리즘으로 최적해를 찾을 수 있습니다.
코드
const int VSIZE = 1e4 + 4;
const int ESIZE = 1e5 + 4;
struct UnionFind {
int parent[VSIZE];
void init(int N) {
for (int i = 1; i <= N; i++)
parent[i] = i;
}
int find(int x) { return parent[x] == x ? x : parent[x] = find(parent[x]); }
void _union(int a, int b) {
a < b ? parent[b] = a : parent[a] = b;
}
}uf;
struct Edge {
int x, y, cost;
bool operator<(Edge O) {
return cost < O.cost;
}
}edge[ESIZE];
struct Sort {
Edge temp[ESIZE];
void merge(int l, int m, int r) {
int i = l, j = m + 1, k = l;
while (i <= m && j <= r)
temp[k++] = edge[i] < edge[j] ? edge[i++] : edge[j++];
while (i <= m) temp[k++] = edge[i++];
while (j <= r) temp[k++] = edge[j++];
for (int idx = l; idx <= r; ++idx)
edge[idx] = temp[idx];
}
void divide(int l, int r) {
if (l == r) return;
int m = l + r >> 1;
divide(l, m);
divide(m + 1, r);
merge(l, m, r);
}
void sort(int E) {
divide(0, E - 1);
}
}sort;
struct MST {
int solve(int V, int E) {
sort.sort(E);
uf.init(V);
int ret = 0;
for (int i = 0, cnt = 1; cnt < V; ++i) {
int x = uf.find(edge[i].x);
int y = uf.find(edge[i].y);
if (x == y) continue;
ret += edge[i].cost;
++cnt;
uf._union(x, y);
}
return ret;
}
}mst;
프림 알고리즘 (Prim Algorithm)
작동 과정
- 임의의 정점을 선택하여 비어있는 최소 스패닝 트리 T에 포함시킴
- 모든 노드가 T에 포함될 때 까지 아래 과정을 반복
- T에 있는 노드와 T에 없는 노드 사이의 간선 중 가중치가 최소인 간선을 찾음
- 해당 간선이 연결하는 두 노드 중에서 T에 없는 노드를 T에 포함시킴

최소 스패닝 트리 T에 포함된 노드를 빨간색,
T에 포함되지 않은 노드를 파란색이라고 두었습니다.
그리고 T에 있는 노드와 T에 없는 노드 사이의 간선을 빨간색으로 두었습니다.
노드 1을 최소 스패닝 트리 T에 포함시키고 시작하겠습니다.
빨간색 간선의 비용 {6, 12} 중 6이 제일 작습니다.
간선 (1, 4, 6)을 채택하고 T에 노드 4를 포함시킵니다.

T에 포함된 간선을 초록색으로 두었습니다.
빨간색 간선의 비용 {12, 7, 9} 중 7이 제일 작습니다.
T에 노드 3을 포함시킵니다.

빨간색 간선의 비용 {12, 9, 3, 1} 중 1이 제일 작습니다.
T에 노드 2를 포함시킵니다.
만약, 비용이 12인 간선이 제일 작다고 가정하면 어떻게 하면 될까요?
이 간선이 연결하는 1번과 3번 노드는 이미 T에 포함되어 있기 때문에 간선을 포함하지 않고 넘어가면 됩니다.

{12, 9, 3, 5} 중 3이 제일 작습니다.
T에 노드 5를 포함시킵니다.

모든 노드가 포함되어서 종료합니다.
위의 크루스칼 알고리즘으로 구한 최소 스패닝 트리의 비용과 똑같다는 것을 알 수 있습니다.
시간 복잡도
최소 비용 간선을 찾을 때는 최소 힙 자료구조를 사용하면 됩니다.
그럼 다익스트라 알고리즘과 똑같은 원리가 되며 최종 시간 복잡도는 아래와 같습니다.
=> O(E log V) (E : 간선의 개수, V : 정점의 개수)
증명
이 방법 역시 매 순간 적은 비용의 간선을 보기 때문에 그리디 알고리즘 입니다.
그러므로 위에서 증명했던 귀류법으로 똑같이 증명할 수 있습니다.
귀류법
- 프림 알고리즘에 선택되는 간선이 최소 스패닝 트리 T에 포함되지 않는다
위의 가정에 맞는 간선을 e1 : (u, v, cost) 라고 두겠습니다.
u와 v를 연결하는 최소 스패닝 트리 T의 경로 상에 적어도 하나는 cost 보다 크거나 같은 간선이 존재합니다.
- 경로 상의 모든 간선이 다 작다면, 프림 알고리즘이 이전에 선택했을 것입니다.
이 간선을 제외하고 e1을 추가하면 최소 스패닝 트리 T의 비용이 줄거나 같아집니다.
손해보지 않기 때문에 위의 알고리즘이 정당합니다.
코드
const int VSIZE = 1e4 + 4;
const int ESIZE = 1e5 + 4;
struct Pair {
int x, y;
bool operator<(Pair O) {
return y < O.y;
}
};
struct Vector {
Pair* arr;
int sz, cap;
void push(Pair p) {
if (++sz > cap) {
cap += 10;
arr = (Pair*)realloc(arr, sizeof(Pair) * cap);
}
arr[sz - 1] = p;
}
int getSize() { return sz; }
Pair operator[](int idx) { return arr[idx]; }
}adj[VSIZE];
struct PQ {
Pair arr[ESIZE];
int top = -1;
void up() {
int cha = top;
Pair val = arr[cha];
while (cha > 0) {
int p = cha - 1 >> 1;
if (arr[p] < val) break;
else {
arr[cha] = arr[p];
cha = p;
}
}
arr[cha] = val;
}
void down() {
int cha = 0;
Pair val = arr[cha];
while (cha <= top) {
int l = cha << 1 | 1;
int r = cha * 2 + 2;
int c = cha;
if (l <= top && arr[l] < arr[c]) c = l;
if (r <= top && arr[r] < arr[c]) c = r;
if (cha == c) break;
else {
arr[cha] = arr[c];
arr[c] = val;
cha = c;
}
}
}
void push(Pair p) {
arr[++top] = p;
up();
}
Pair pop() {
Pair ret = arr[0];
arr[0] = arr[top--];
down();
return ret;
}
bool empty() { return top == -1; }
}pq;
struct MST {
bool T[VSIZE];
void push(int n) {
T[n] = true;
for (int i = 0; i < adj[n].getSize(); i++) {
if (!T[adj[n][i].x]) {
pq.push(adj[n][i]);
}
}
}
int solve(int V, int E) {
int ret = 0, cnt = 1;
push(1);
while (!pq.empty() && cnt < V) {
Pair cur = pq.pop();
if (T[cur.x]) continue;
++cnt;
ret += cur.y;
push(cur.x);
}
return ret;
}
}mst;두 알고리즘 비교
- 크루스칼 알고리즘은 간선 기반 알고리즘,
- 프림 알고리즘은 정점 기반 알고리즘 입니다.
간선이 많은 그래프에서는 프림 알고리즘이 유리하며,
간선이 적은 그래프에서는 크루스칼 알고리즘이 유리합니다.
백준 문제 1197 최소 스패닝 트리 문제를 두 알고리즘으로 풀어봤습니다.
두 알고리즘의 걸린 시간이 똑같이 나왔습니다.

그렇지만 위에서 설명한 대로 문제의 간선 개수를 확인한 뒤에 적절한 알고리즘을 사용하면 좋을 것입니다.
문제
기본 문제 : https://www.acmicpc.net/problem/1197
응용 문제 : https://www.acmicpc.net/problem/2887
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
2887번: 행성 터널
첫째 줄에 행성의 개수 N이 주어진다. (1 ≤ N ≤ 100,000) 다음 N개 줄에는 각 행성의 x, y, z좌표가 주어진다. 좌표는 -109보다 크거나 같고, 109보다 작거나 같은 정수이다. 한 위치에 행성이 두 개 이
www.acmicpc.net
참고 자료
개념 : https://www.youtube.com/watch?v=tKwnms5iRBU
kruskal : https://blog.naver.com/kdr06006/221756452354
prim : https://www.weeklyps.com/entry/프림-알고리즘-Prims-algorithm
증명 : 알고리즘 문제해결전략 - 구종만
감사합니다.
'알고리즘 & 자료구조' 카테고리의 다른 글
| 2-SAT (0) | 2023.07.24 |
|---|---|
| 강한 연결 요소 (Strongly Connected Component) (0) | 2023.07.20 |
| A* algorithm (0) | 2023.07.07 |
| Topological Sort (위상 정렬) (0) | 2023.06.29 |
| Disjoint-set (0) | 2023.06.27 |



