안녕하세요.
오늘은 A* algorithm (A star algorithm) 에 대해 알아보겠습니다.
최단 경로 휴리스틱 알고리즘
시작 정점 s에서 끝 정점 e 까지의 최단 경로를 근사화한 값을 구하기 위한 최단 경로 알고리즘 입니다.
휴리스틱 알고리즘 중 하나 입니다.
최단 경로를 찾는데 가장 유명한 알고리즘이 다익스트라 알고리즘 입니다.
다익스트라 알고리즘은 시작 정점에서 현재 정점까지 걸린 비용이 작은 것을 우선으로 탐색합니다.
A* algorithm은 f cost가 작은 것을 우선으로 탐색합니다.
f cost = g cost + h cost
g cost = 시작 정점에서 현재 정점까지 걸린 비용
h cost = 현재 정점에서 끝 정점까지 걸릴 예상 비용
g cost가 다익스트라 알고리즘에서 우선시하는 비용인 시작 정점에서 현재 정점까지 걸린 비용입니다.
A* algorithm은 여기에 h cost 라는 것을 더한 비용을 확인합니다.
모든 노드의 h cost를 0으로 둔다면 f cost = g cost가 됩니다.
이는 다익스트라 알고리즘과 똑같은 비용입니다.
=> 다익스트라 알고리즘과 A* algorithm의 차이는 h cost 뿐 입니다.
(다익스트라 알고리즘 설명 : https://blog.naver.com/kdr06006/221780930566)
다익스트라 (Dijkstra Algorithm)
안녕하세요. 오늘은 다익스트라에 대해 포스팅 하겠습니다. 다익스트라 알고리즘은 하나의 정점으로부터 다...
blog.naver.com
h cost는 끝 정점까지 걸릴 비용을 예측하는 것으로, 이로 인해 답과 인접한 근사치를 구할 수 있습니다.
h cost를 어떻게 잡냐에 따라 알고리즘 성능이 좌우되므로, 매우 중요한 휴리스틱 값입니다.
h cost 구하기

h cost를 설명하는 자료 중 인상 깊은 자료가 있어 들고왔습니다.
미로에서 쥐가 치즈를 찾으러 갈 때, 어떤 방법을 사용할 수 있을까요?
1. 그냥 탐색
미로의 동서남북 4방향을 다 탐색해보면서 그냥 다 가보는 방식입니다.
이는 벽이나 도착점을 만날 때 까지 직접 가봐야 알 수 있습니다.
2. 후각을 사용해 치즈의 냄새를 쫓아감
냄새는 거리가 가까워질 수록 더 강하게 납니다.
쥐는 냄새를 이용해 치즈를 빠르게 찾을 수 있습니다.
도착점까지 가까워질 수록 냄새가 더 강하게 나고, 냄새가 이끄는 대로 따라가면 됩니다.
이 냄새가 바로 h cost가 됩니다.
그렇다면 저희는 어떻게 h cost를 정할 수 있을까요?

2차원 좌표 상에서 h cost를 정해보겠습니다.
여러 방법이 있을 수 있지만, 대표적으로 많이 사용되는 2가지 방법을 알아보겠습니다.
1. Manhattan distance
두 노드의 x 좌표의 차이 + y 좌표의 차이의 합으로 구합니다.

두 노드의 x 좌표의 차이는 1,
두 노드의 y 좌표의 차이는 4 입니다.
h cost = 1 + 4 = 5로 설정할 수 있습니다.
2. Euclidean distance
좌표 상의 실제 거리인 sqrt(x좌표 차이 ^ 2 + y 좌표 차이 ^ 2)로 구합니다.
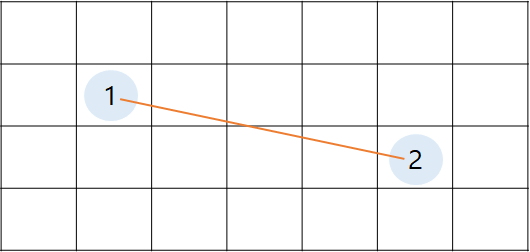
1번 노드와 2번 노드의 직선 거리를 h cost로 설정합니다.
h = sqrt(1 + 16)
과정
아래 사이트의 수도 코드를 참고해 작성했습니다.
https://www.geeksforgeeks.org/a-search-algorithm/
A* Search Algorithm - GeeksforGeeks
A* Search algorithm is one of the best and popular technique used in path-finding and graph traversals.
www.geeksforgeeks.org
1. open list, closed list를 준비
2. start node를 open list에 넣기
(start node는 f 값을 0으로 둬도 상관 없음)
3. open list가 빌 때 까지 반복
a) open list에서 f 값이 가장 작은 노드를 찾기 => current node
b) current node가 target node 이면, return_value 갱신
c) current node를 closed list에 넣기
d) current node를 open list에서 삭제
e) 인접한 노드 (4방향, 6방향, 8방향... 문제에 따라 다름) 를 탐색
-> neighbor node
i) neighbor node의 f cost와 계산하기
if) neighbor node가 open list에 들어있고, f cost가 더 작다면
continue
else if) neighbor node가 closed list에 들어있고, f cost가 더 작다면
continue
else) open list에 neighbor node와 f cost 넣기
return return_value
이 수도 코드를 바탕으로 그림과 함께 A* algorithm의 작동 과정을 알아보겠습니다.
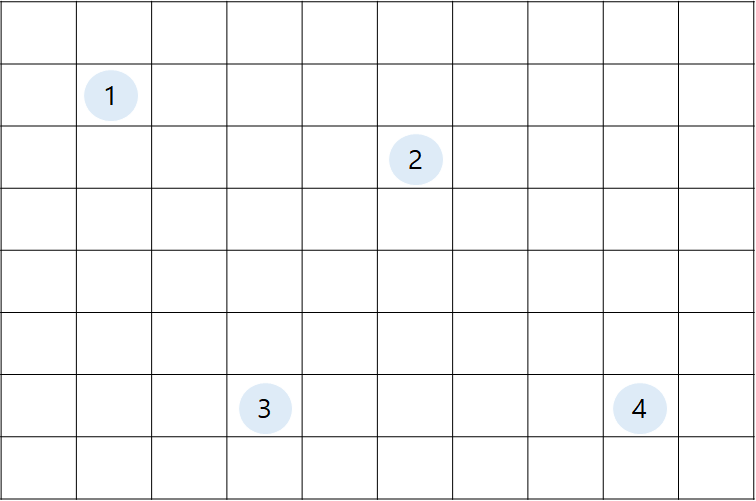
2차원 격자에 4개의 노드가 있다고 가정하겠습니다.
시작 정점을 1, 도착 정점을 4로 두겠습니다.
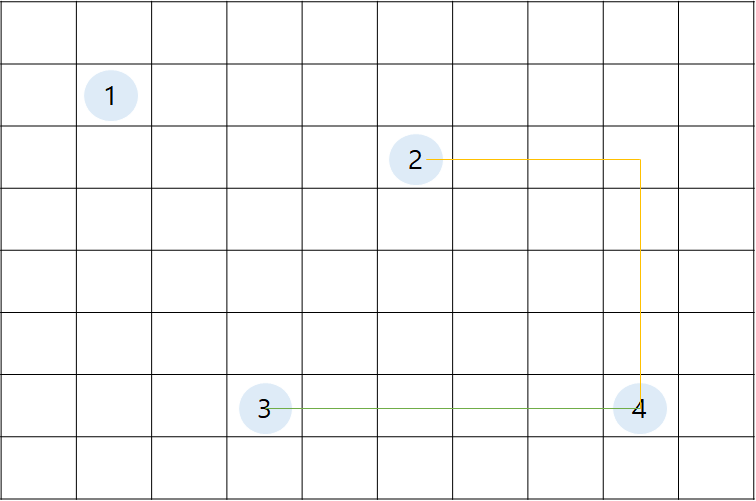
h cost 값은 도착 정점까지의 x 좌표 차이와 y 좌표 차이의 합으로 계산하겠습니다.
h(1) = 시작 정점이므로 따로 구하지 않음
h(2) = 4 + 3 = 7
h(3) = 0 + 5 = 5
h(4) = 0
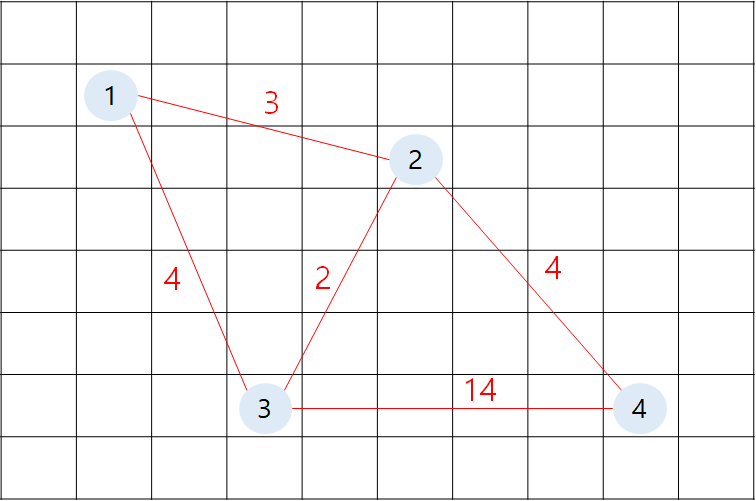
각 노드를 연결시켜주는 간선이 이렇게 있다고 가정하겠습니다.
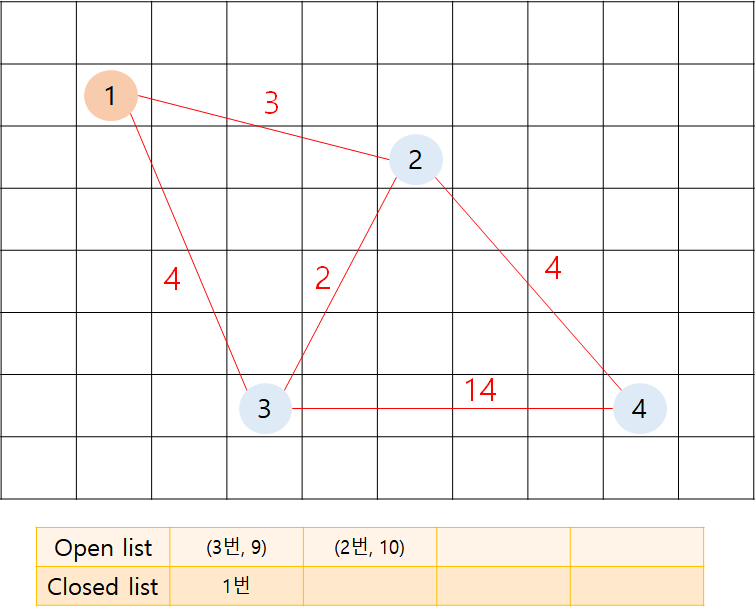
1번 노드부터 탐색을 시작합니다.
closed list에 1번 노드가 담깁니다.
1번 노드의 인접 정점을 확인합니다.
f(2) = g cost + h cost = 3 + 7 = 10
f(3) = g cost + h cost = 4 + 5 = 9
=> 2번과 3번 노드가 open list에 들어갑니다.
open list에는 f cost가 작은 순으로 정렬 됩니다.
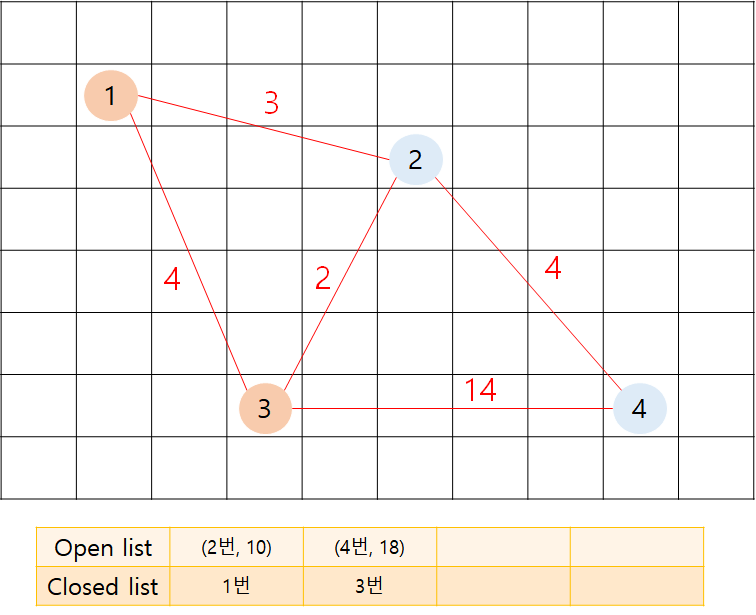
open list에서 가장 f 값이 작은 3번 노드를 추출합니다.
closed list에 3번 노드가 담깁니다.
3번 노드의 인접 정점을 확인합니다.
f(1) = g cost + h cost = 8 + 0 = 8
f(2) = g cost + h cost = 6 + 7 = 13
f(4) = g cost + h cost = 18 = 0 = 18
=> 1번과 2번 노드는 open과 closed list에 이미 더 작은 값으로 들어갔기 때문에 open list에 넣지 않습니다.
=> 4번 노드는 open list에 넣습니다.
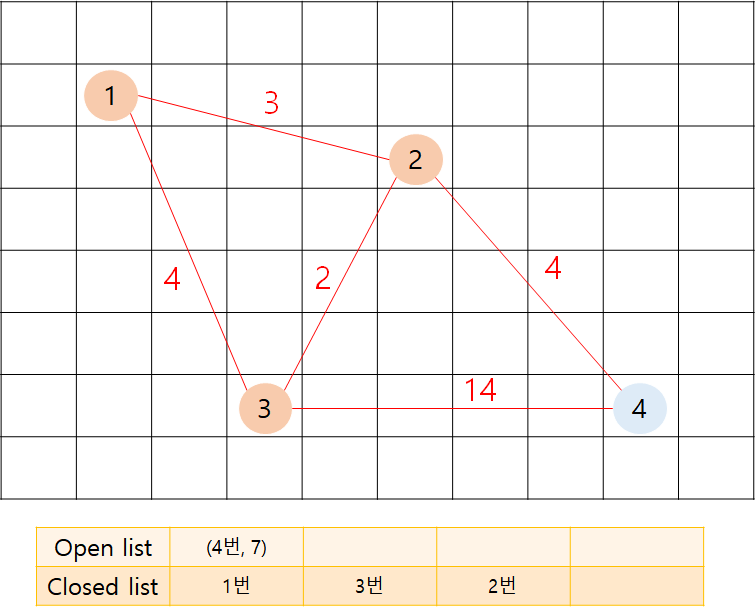
open list에서 가장 f cost가 작은 2번 노드를 추출했습니다.
2번의 인접 노드를 보면 아래와 같습니다.
f(1) = g cost + h cost = 6 + 0 = 6
f(3) = g cost + h cost = 5 + 5 = 10
f(4) = g cost + h cost = 7 + 0 = 7
=> 4번 노드의 가중치가 18에서 7로 갱신됩니다.
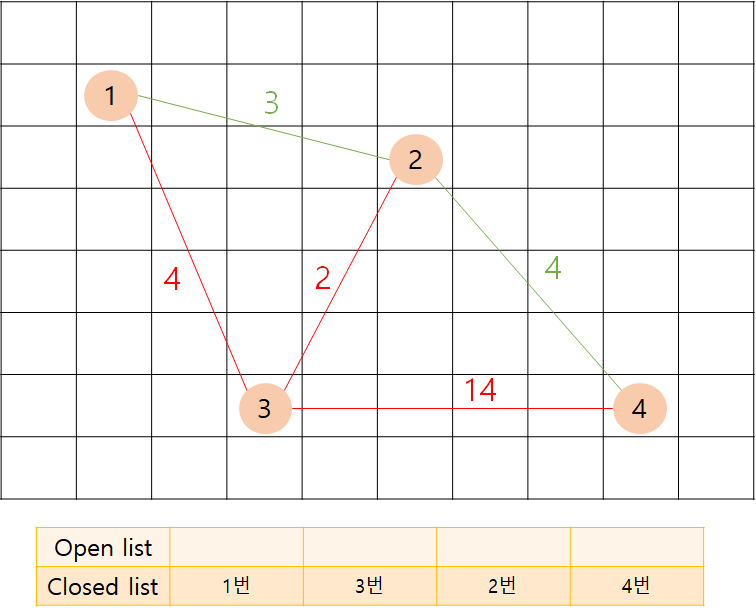
마지막 4번 노드까지 탐색하고 인접한 정점을 봅니다.
인접한 정점이 모두 open list나 closed list에 더 작은 값으로 들어있기 때문에 open list에 아무것도 넣지 않습니다.
그리고 open list는 비어있기 때문에 종료됩니다.
위의 그림에서 초록색 간선 경로를 따라가면 최단 경로가 나옵니다.
(1 -> 2 -> 4)
다익스트라 알고리즘과 다르게 A* algorithm은 도착 정점에 도달해도 탐색을 계속 이어나가야 합니다.
f cost가 작은 순으로 탐색을 하기 때문입니다.
2번 노드의 h cost를 터무니 없이 크게 잡는다면 탐색 노드 순서는 아래와 같습니다.
1번 노드 -> 3번 노드 -> 4번 노드 -> 2번 노드 -> 3, 4번 노드
f cost는 크지만, 우리가 구하고자 하는 값은 g cost 이기에 open list에 원소가 없을 때까지 탐색을 계속 해야합니다.
속도 비교
아래 사이트는 여러 길찾기 알고리즘의 시각화 사이트입니다.
https://qiao.github.io/PathFinding.js/visual/
PathFinding.js
qiao.github.io
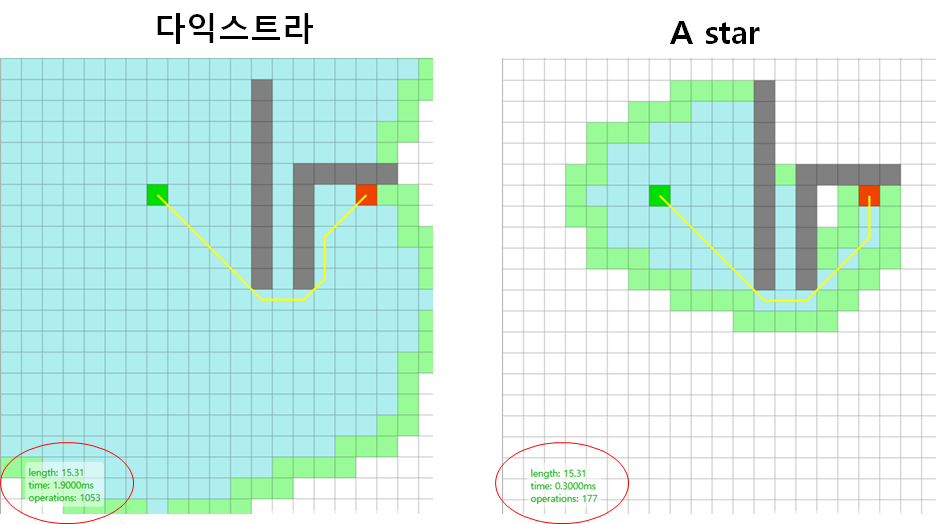
다익스트라 알고리즘과 A* (A star) algorithm의 속도를 비교한 결과입니다.
훨씬 더 적은 노드를 탐색하고 금방 target node 까지 도달한 것을 확인할 수 있습니다.
이러한 성능적인 측면으로, A* algorithm이 지도 상의 길찾기 기능이나 게임의 길찾기 기능에 많이 사용된다고 알려져 있습니다.
참고 자료
다익스트라 : https://blog.naver.com/kdr06006/221780930566
A* algorithm : https://www.geeksforgeeks.org/a-search-algorithm/
휴리스틱 : https://www.youtube.com/watch?v=71CEj4gKDnE
감사합니다.
'알고리즘 & 자료구조' 카테고리의 다른 글
| 2-SAT (0) | 2023.07.24 |
|---|---|
| 강한 연결 요소 (Strongly Connected Component) (0) | 2023.07.20 |
| 최소 스패닝 트리 (Minimun Spanning Tree) (0) | 2023.07.14 |
| Topological Sort (위상 정렬) (0) | 2023.06.29 |
| Disjoint-set (0) | 2023.06.27 |



