안녕하세요.
오늘은 2-Satisfiability 에 대해 알아보겠습니다.
개념
전체 식이 True가 되도록 변수에 True 또는 False 값을 배정하는 문제입니다.
True 또는 False 2지 선다이기 때문에 2-SAT 이라 불립니다.

X, Y, Z 변수에 True 또는 False 값을 할당해 전체 라인이 True가 되도록 만들어봅시다.
- Line 1
- X : True, Y : False, Z : False
- 가능
- Line 2
- X에 True 또는 False 를 넣어도 만족하지 않음
- 불가능
풀이
그래프 모델링을 통해 2-SAT을 풀 수 있습니다.

(X or Y)
X 또는 Y가 true가 되어야 합니다.
만약 X가 false 라면, Y는 반드시 true가 되어야 합니다. (not X -> Y)
만약 Y가 false 라면, X는 반드시 true가 되어야 합니다. (not Y -> X)
이를 그래프 모델링을 하면 아래와 같이 나옵니다.

(!Y or Z)
!Y 또는 Z가 true가 되어야 합니다.
만약 !Y가 false 라면, Z는 true가 되어야 합니다. (Y -> Z)
만약 Z가 false 라면, !Y는 true가 되어야 합니다. (not Z -> not Y)
이를 그래프 모델링하면 아래와 같이 나옵니다.

Line 1, Line 2에 그래프 모델링을 적용하면 아래와 같이 그래프가 나옵니다.

이렇게 그래프 모델링을 마치면 해당 라인이 True가 되는지 여부를 쉽게 파악할 수 있습니다.
임의의 정점 u와 not u가 같은 SCC에 속하면 해당 라인을 True로 만들 수 없습니다.
같은 SCC 내의 모든 정점은 같은 값을 대입 받아야 합니다.
그런데 정점 u와 not u가 같은 값을 받을 수는 없습니다.
Line 2를 보면 x와 !x가 같은 SCC 입니다.
그렇기에 Line 2를 True로 만들 수 없습니다.
그리고 이런 사이클 추출은 SCC 알고리즘을 사용하면 됩니다.
https://kdr06006.tistory.com/6
강한 연결 요소 (Strongly Connected Component)
안녕하세요. 오늘은 줄여서 SCC 라고도 불리는 강한 연결 요소에 대해 알아보도록 하겠습니다. 사이클 유향 그래프에서 사이클을 찾는 알고리즘을 SCC 알고리즘 이라고 합니다. 하나의 SCC에 속하
kdr06006.tistory.com
변수에 값 대입
사이클이 생기면 해당 라인을 True로 만들 방법이 없다는걸 알았습니다.
그럼 정점 u에 true 또는 false 중 어떤 값을 대입하면 될까요?
명제 p -> q가 참이 될려면 아래 두 개 중 하나를 만족하면 됩니다.
- p가 true, q가 true
- p가 false, q는 아무 값
즉, p에 false 값을 부여해서 손해볼 일이 없습니다.

위와 같은 그래프가 있다고 가정하겠습니다.
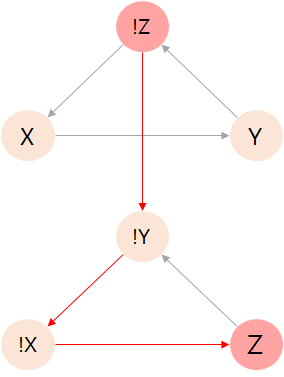
Z 정점을 기준으로 보면,
!Z -> Z 명제가 참이 되어야 합니다.
!Z에 false 값을 부여하면 됩니다.
(Z에 true 값 부여)
만약 반대로 !Z에 true를 부여하면,
!Z -> Z 명제가 거짓이 되면서 해당 라인은 False 값을 가지게 됩니다.
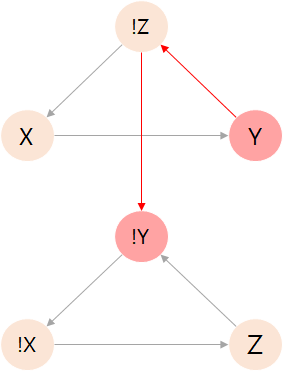
Y 정점을 기준으로 보면,
Y -> !Y 명제가 참이 되어야 합니다.
Y에 false 값을 부여하면 됩니다.
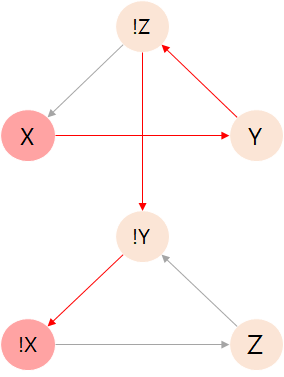
X -> !X 명제가 참이 되어야 합니다.
X에 false 값을 부여하면 됩니다.
정점 u와 not u 사이에 관계가 없다면 어느 값을 부여하면 될까요?
정점 u에 어떤 값을 대입해도 해당 라인에는 영향을 주지 않습니다.
true 또는 false 아무 값이나 대입하면 됩니다.
구현 시에는
SCC 끼리 묶어서 하나의 컴포넌트로 표현한다면, DAG 가 나옵니다.
타잔 알고리즘에서 스택에 빠져나오는 순서대로 SCC 번호를 매겼습니다.
SCC 번호를 역순으로 나열하면 DAG의 간선 방향을 위배하지 않는 위상 정렬이 나옵니다.
sccn[u]를 u의 scc 번호라고 한다면,
- sccn[u] < sccn[!u]
- !u -> u로 연결되는 직/간접적인 간선이 있다는 의미입니다.
- !u에 false 값을 부여하면 됩니다. (u에 true 값을 부여)
- sccn[u] > sccn[!u]
- u -> !u로 연결되는 직/간접적인 간선이 있다는 의미입니다.
- u에 false 값을 부여하면 됩니다.
시간 복잡도
V : 정점의 개수, E : 간선의 개수 라고 한다면
SCC 알고리즘으로 SCC를 추출합니다. -> O(V + E)
2-SAT을 판별하고 모든 변수에 값을 대입합니다. -> O(V)
O(V + E + V) 이므로 최종적으로 O(V + E)가 됩니다.
코드
SCC 알고리즘은 타잔 알고리즘을 사용했습니다.
정점을 true / false 두 정점으로 분류해야 하므로 2 * N 개의 정점이 필요합니다.
( x와 x+N 정점으로 분류 )
인접 리스트는 메모리 풀과 링크드 리스트를 사용했습니다.
#include <cstdio>
const int VSIZE = 2e4 + 4;
const int ESIZE = 2e5 + 4;
struct EdgePool {
EdgePool* next;
int x;
}edge[ESIZE];
int N, edgeCnt;
EdgePool* getEdge(int x) {
edge[edgeCnt].x = x;
return &edge[edgeCnt++];
}
struct Vector {
EdgePool* head;
void push_back(int x) {
EdgePool* cur = getEdge(x);
cur->next = head;
head = cur;
}
}adj[VSIZE];
template <typename T>
struct Stack {
T arr[VSIZE];
int top = -1;
inline bool empty() { return top == -1; }
inline void push(T x) { arr[++top] = x; }
inline T pop() { return arr[top--]; }
};
// !x -> N + x
inline int get(int x) { return x > 0 ? x : -x + N; }
inline int min(int a, int b) { return a < b ? a : b; }
struct SCC {
int dfsn[VSIZE], dfsNumber;
int sccn[VSIZE], sccNumber;
bool finish[VSIZE];
Stack<int> S;
void solve() {
for (register int i = 1; i <= 2 * N; ++i) {
if (dfsn[i] == 0) dfs(i);
}
if (!TOF()) printf("0\n");
else { printf("1\n"); allocate(); }
}
int dfs(int cur) {
int ret = dfsn[cur] = ++dfsNumber;
S.push(cur);
for (EdgePool* e = adj[cur].head; e; e = e->next) {
int n = e->x;
if (!dfsn[n]) ret = min(ret, dfs(n));
else if (!finish[n]) ret = min(ret, dfsn[n]);
}
if (ret == dfsn[cur]) {
++sccNumber;
while (!S.empty()) {
int x = S.pop();
sccn[x] = sccNumber;
finish[x] = true;
if (x == cur) break;
}
}
return ret;
}
bool TOF() {
for (register int i = 1; i <= N; ++i) {
if (sccn[i] == sccn[get(-i)]) return false;
}
return true;
}
void allocate() {
for (register int i = 1; i <= N; ++i) {
printf("%d ", sccn[i] < sccn[get(-i)]);
}
}
}scc;
int main()
{
int M;
scanf("%d %d", &N, &M);
int x, y;
while (M--) {
scanf("%d %d", &x, &y);
// !x -> y, !y -> x
adj[get(-x)].push_back(get(y));
adj[get(-y)].push_back(get(x));
}
scc.solve();
}문제
기본 문제 : https://www.acmicpc.net/problem/11281
11281번: 2-SAT - 4
첫째 줄에 변수의 개수 N (1 ≤ N ≤ 10,000)과 절의 개수 M (1 ≤ M ≤ 100,000)이 주어진다. 둘째 줄부터 M개의 줄에는 절이 주어진다. 절은 두 정수 i와 j (1 ≤ |i|, |j| ≤ N)로 이루어져 있으며, i와 j가
www.acmicpc.net
응용 문제 1 : https://www.acmicpc.net/problem/3648
3648번: 아이돌
각 테스트 케이스에 대해서, 상근이를 포함해, 다음 라운드 진출 목록을 심사위원의 의심 없이 만들 수 있으면 'yes'를, 없으면 'no'를 출력한다.
www.acmicpc.net
응용 문제 2 : https://www.acmicpc.net/problem/20942
20942번: 신촌지역 초중고등학생 프로그래밍 대회 동아리 연합 대회
첫 번째 자리에는 $15$세의 참가자가 이미 배치되어 있다. 두 번째, 세 번째, 네 번째 자리에 각각 $17$세, $12$세, $19$세의 참가자를 배치하면, $15 \operatorname{\&} 17 = 1$, $15 \operatorname{\&} 12 = 12$, $12
www.acmicpc.net
참고 자료
https://blog.naver.com/kdr06006/222844956254
2-SAT (2-Satisfiability)
안녕하세요. 오늘은 2-SAT에 대해 알아보겠습니다. Satisfiability라 하면 조금 생소한 단어인데요. 2-...
blog.naver.com
감사합니다.
'알고리즘 & 자료구조' 카테고리의 다른 글
| 냅색 (Knapsack) (0) | 2023.08.13 |
|---|---|
| LIS (Longest Increasing Sequence) (0) | 2023.08.02 |
| 강한 연결 요소 (Strongly Connected Component) (0) | 2023.07.20 |
| 최소 스패닝 트리 (Minimun Spanning Tree) (0) | 2023.07.14 |
| A* algorithm (0) | 2023.07.07 |



