안녕하세요.
Disjoint-set에 대해 알아보도록 하겠습니다.
서로소 집합, 분리 집합
Disjoint-set은 서로 공통된 원소를 가지고 있지 않은 두 개 이상의 집합입니다.

서로 다른 원소들이 같은 집합에 있는지, 혹은 다른 집합에 있는지를 판별할 수 있습니다.
트리 형태로 관리하며, 연산이 union과 find 두 가지가 있기에 union-find 라고도 불립니다.
과정
어떤 알고리즘을 거쳐서 disjoint-set이 같은 집합에 속하는지를 판별할 수 있는지 알아보겠습니다.
1) parent 배열 준비
parent 배열이란, parent(x)의 값은 x의 부모 노드를 의미합니다.
처음에는 모든 노드가 자기 자신이 루트 노드인 트리이므로 아래와 같이 설정해줍니다.


2) union 연산
union 연산은 서로 다른 두 집합을 하나로 합치는 과정입니다.
union(a, b)를 하게 되면, a의 루트와 b의 루트를 한 집합으로 묶는 것입니다.
예를 들어 union(2, 3)과 union(1, 3)을 순차적으로 진행하게 되면 parent 배열과 트리는 아래와 같이 구성됩니다.


3) find 연산
find(x)는 x가 속한 트리의 루트 노드를 찾는 것입니다.
즉, x의 1대 조상 노드를 반환해줍니다.
위의 그림과 같이 한 줄로 치우쳐진 트리가 만들어지면 find 연산의 시간 복잡도는 어떻게 될까요?
N개의 노드가 한 줄로 이어지면, 부모 노드를 N번 만큼 찾아줘야 합니다.
시간 복잡도는 O(N) 입니다.
4) 코드
const int SIZE = 1e4 + 4;
struct UnionFind {
int parent[SIZE];
void init(int N) {
for (int i = 1; i <= N; i++) parent[i] = i;
}
int find(int x) {
if (x == parent[x]) return x;
return find(parent[x]);
}
void _union(int a, int b) {
a = find(a);
b = find(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
};시간을 줄이기 위한 3가지 방법
find 연산의 시간 복잡도를 줄이기 위해 3가지 방법이 있습니다.
1) Path-Compression Union Find
2) Rank-Compression Union Find
3) Weighted Union Find
이 3가지 방법을 알아보도록 하겠습니다.
1) Path-Compression Union Find
3가지 방법 중에서 가장 빠른 시간 복잡도를 자랑하는 알고리즘 입니다.
find(x) 연산에서 x의 부모 노드부터 루트 노드까지 가는 모든 노드를 루트의 바로 아래 자식으로 갱신하는 것입니다.
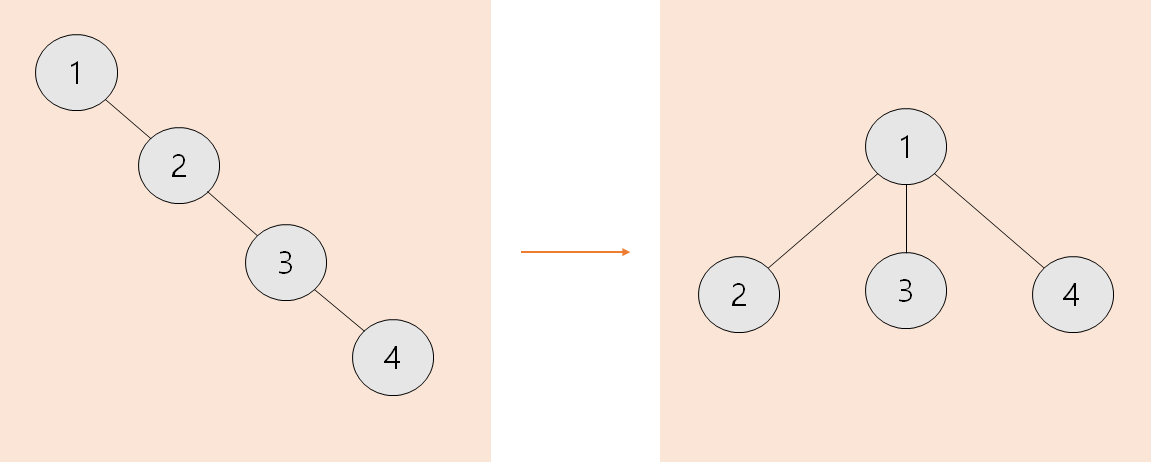
기존의 방식에서 코드를 한 줄만 바꿔주면 됩니다.
int find(int x) {
if (x == parent[x]) return x;
return parent[x] = find(parent[x]);
}
find와 union 연산을 삼항 연산자로 줄일 수 있습니다.
이를 적용하면 코드가 훨씬 간결해집니다.
const int SIZE = 1e4 + 4;
struct UnionFind {
int parent[SIZE];
void init(int N) {
for (int i = 1; i <= N; i++) parent[i] = i;
}
inline int find(int x) { return x == parent[x] ? x : parent[x] = find(parent[x]); }
void _union(int a, int b) {
a = find(a);
b = find(b);
a < b ? parent[b] = a : parent[a] = b;
}
};
시간 복잡도는 amortized(분할 상환) O(α(n)) 입니다.
- amortized (분할 상환) : 시간 또는 비용을 평균적으로 분석하는 기법
(최악의 경우는더 많은 비용이 들지만, 평균적으로 이만큼 걸린다) - α(n) : Ackermann 함수의 역함수 ⇒ 매우 느리게 증가하는 함수
Ackermann 함수란? 두 자연수 m, n에 대하여 아래와 같이 정의됨
A(m, n) = n + 1, if m = 0
A(m, n) = A(m-1, 1), if m > 0 and n = 0
A(m, n) = A(m-1, A(m, n-1)), if m > 0 and n > 0
아커만 함수는 간단한 정의로 시작하지만 매우 빠르게 증가하는 함수 실제로 작은 입력에도 매우 큰 값을 생성함 예를 들어, A(3, 3)의 값은 29,765이다.
Ackermann 함수의 역함수는 아주 느리게 증가하는 함수로 사실상 1에 수렴한다고 생각하면 됩니다.
그래서 최종 시간 복잡도는 amortized O(1) 입니다.
2) Rank-Compression Union Find
이 방법은 아까와 다르게 find 연산은 차이가 없습니다.
대신, union 연산에서 차이가 있습니다.
각각의 집합이 존재합니다.
이 집합은 트리의 형태로 관리가 되는데, 트리라면 높이(level)가 존재합니다.
Union 과정에서 항상 높이가 더 낮은 트리를 높은 트리 밑으로 넣어줍니다.
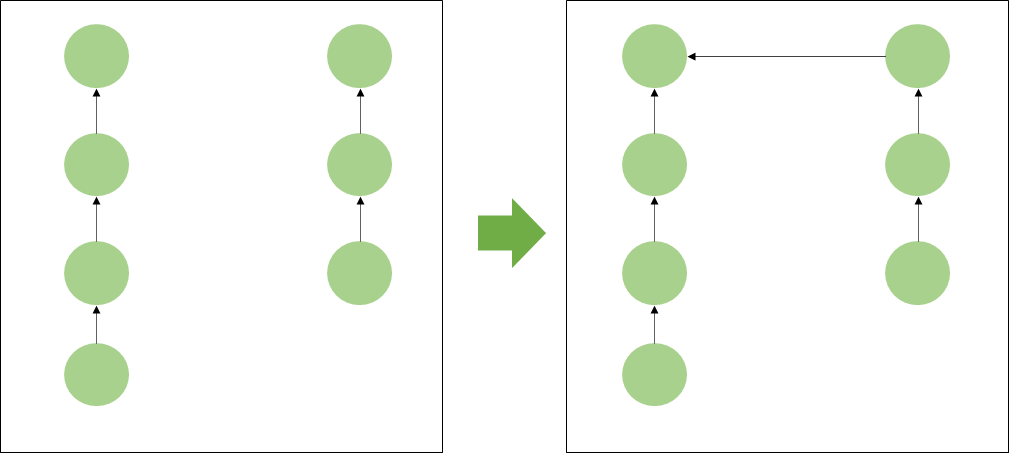
왼쪽 집합은 높이가 4인 트리입니다.
오른쪽 집합은 높이가 3인 트리입니다.
서로 다른 두 트리를 합칠 때는 높이가 더 낮은 트리를 높은 트리 밑으로 넣어줍니다.
즉, 높이가 3인 트리를 높이가 4인 트리 밑으로 집어넣어 줍니다.
위의 그림은 이해를 돕기 위한 예시 그림으로, 실제로 rank-compression 기법을 쓰면 한 줄로 치우쳐진 트리가 나오지 않습니다.
합쳐진 트리의 높이는 두 트리의 높이가 같을 때만 증가합니다.
높이가 3인 트리가 두 개 있었다면, 높이가 4인 트리로 합쳐지겠죠.
그리고 높이가 h가 되기 위해 최소 x개의 노드가 필요하다고 가정하겠습니다.
그러면 높이가 h+1이 되기 위해서는 최소 2x개의 노드가 필요합니다.
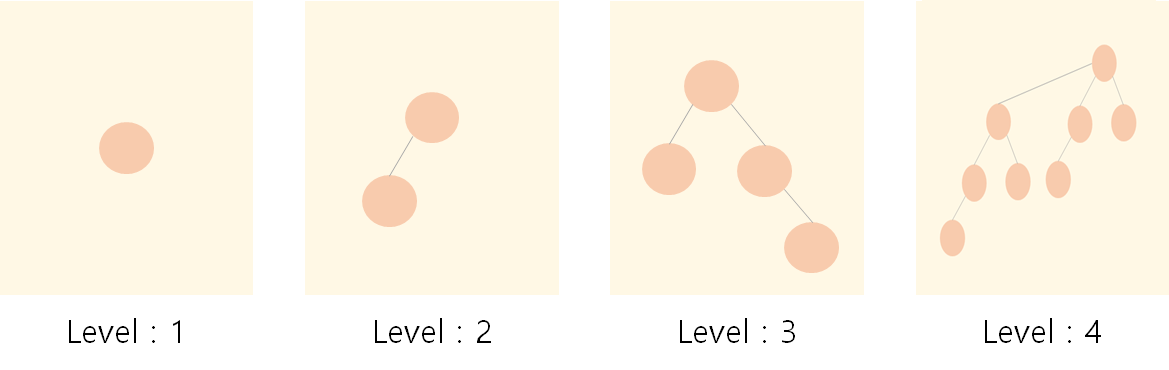
level이 1 증가함에 따라 필요한 노드의 수는 2배가 됨을 알 수 있습니다.
트리의 높이는 노드의 수의 로그에 비례합니다.
그래서 find 연산의 시간 복잡도는 O(log N)이 됩니다.
const int SIZE = 1e6 + 4;
struct UnionFind {
int parent[SIZE];
int height[SIZE];
void init(int N) {
for (int i = 1; i <= N; i++) {
parent[i] = i;
height[i] = 1;
}
}
int find(int x) {
if (x == parent[x]) return x;
return find(parent[x]);
}
void _union(int a, int b) {
a = find(a);
b = find(b);
if (a == b) return;
if (height[a] == height[b]) ++height[a];
if (height[a] < height[b]) parent[a] = b;
else parent[b] = a;
}
};
이 방법은 첫 번째 방법보다 단점이 2가지 존재합니다.
위의 두 제출 내용이 rank-compression 방식,
아래 두 제출 내용이 path-compression 방식 입니다.

1) 시간이 더 느립니다.
둘 다 빠른 시간 복잡도는 맞습니다.
하지만 첫 번째 방법이 시간이 조금 더 빠른 것을 확인할 수 있습니다.
2) 메모리 사용량이 더 큽니다.
parent 배열 말고도 level 배열이 있어야 하기에 메모리가 더 소모 됩니다.
그렇지만, 이런 담점이 존재함에도 사용해야하는 case가 있습니다.
union 과정을 특정 시점으로 되돌리는 roll back을 하고 싶을 때 사용합니다.
path-compression은 한 번의 find 과정에서 많은 노드들의 parent 값이 갱신됩니다.
하지만 rank-compression 방식은 한 번의 union 과정에서 한 번의 parent 값만 갱신되므로 roll back 하기에 수월합니다.
이러한 roll back은 Offline Dynamic Connectivity 기법에서 사용됩니다.
자세한 내용은 제가 이전에 네이버 블로그에서 작성했던 글을 참고해주시면 감사하겠습니다.
(https://blog.naver.com/kdr06006/222079403088)
3) Weighted Union Find
이 방법은 앞의 두 가지 방법과 다르게 해당 노드가 속한 트리의 size까지 알고 싶을 때 사용합니다.
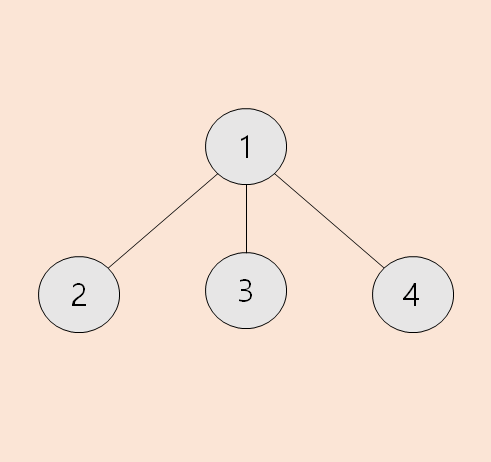
2번 노드가 속해있는 트리의 size는 4입니다.
노드의 parent 정보 뿐만 아니라, size까지 알고 싶을 때 빠르게 찾을 수 있는 알고리즘입니다.
두 가지 정보를 알아야 하기에 parent 배열 + size 배열 까지 총 2 가지 배열이 존재해야 합니다.
하지만 parent 배열 하나만으로 해결이 가능합니다.
parent 배열에는 아래와 같이 저장합니다.
- 루트 노드라면, -(트리의 크기)
- 루트 노드가 아니라면, 부모 노드를 저장
1) 초기화 과정
parent 배열을 전부 -1로 초기화 해줍니다.
처음에는 모든 노드가 루트 노드이기에, -(트리의 크기)를 저장해주는 것입니다.
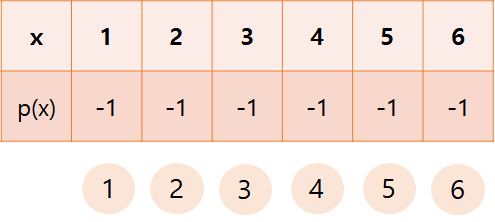
2) union
덩치가 더 작은 트리를 덩치가 큰 트리에 합쳐줍니다.
즉, size가 작은 트리를 size가 큰 트리에 합쳐주는 것입니다.
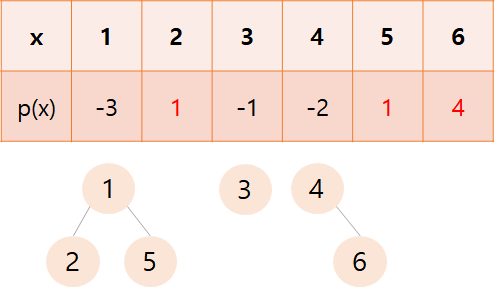
루트 노드에는 -(트리의 크기),
루트 노드가 아니면 부모 노드를 저장합니다.
2번, 5번, 6번 노드에는 각각 부모 노드가 저장된 것을 확인할 수 있습니다.
위의 rank compression 방법과 똑같습니다.
그리고 find 연산 역시 시간 복잡도는 O(log N) 입니다.
3) find
음수가 나올 때 까지 부모 노드로 올라갑니다.
음수가 나오면, 현재 노드가 루트 노드가 됩니다.
+) path-compression과 같이 사용 가능합니다.
그럴 경우 find의 시간 복잡도는 amortized O(1) 이 됩니다.
const int SIZE = 1e6 + 4;
struct UnionFind {
int parent[SIZE];
void init(int N) {
for (int i = 1; i <= N; i++) parent[i] = -1;
}
int find(int x) {
if (parent[x] < 0) return x;
return find(parent[x]);
}
void _union(int a, int b) {
a = find(a);
b = find(b);
if (a == b) return;
// 작은 트리를 큰 트리에 합쳐줌
if (-parent[a] > -parent[b]) { // b가 속한 트리의 크기가 더 작음
parent[a] += parent[b];
parent[b] = a;
}
else {
parent[b] += parent[a];
parent[a] = b;
}
}
};문제
기본 : https://www.acmicpc.net/problem/1717
1717번: 집합의 표현
초기에 $n+1$개의 집합 $\{0\}, \{1\}, \{2\}, \dots , \{n\}$이 있다. 여기에 합집합 연산과, 두 원소가 같은 집합에 포함되어 있는지를 확인하는 연산을 수행하려고 한다. 집합을 표현하는 프로그램을 작
www.acmicpc.net
응용 : https://www.acmicpc.net/problem/2463
2463번: 비용
첫 번째 줄에 정점의 수 N (1< ≤ N ≤ 100,000)과 간선의 수 M (1 ≤ M ≤ 100,000)이 빈칸을 사이에 두고 주어진다. 다음 M개의 각 줄에 간선 하나에 대한 정보를 나타내는 세 개의 양의 정수 x,y,w가 빈칸
www.acmicpc.net
참고 자료
개념 : https://yoongrammer.tistory.com/102
시각화 : https://www.cs.usfca.edu/~galles/visualization/DisjointSets.html
코드 : https://blog.naver.com/kdr06006/221747725360
rank-compression : https://blog.naver.com/kdr06006/222079403088
weighted : https://ssungkang.tistory.com/entry/Algorithm-유니온-파인드Union-Find
Ackermann 함수 : https://ko.wikipedia.org/wiki/아커만_함수
감사합니다.
'알고리즘 & 자료구조' 카테고리의 다른 글
| 2-SAT (0) | 2023.07.24 |
|---|---|
| 강한 연결 요소 (Strongly Connected Component) (0) | 2023.07.20 |
| 최소 스패닝 트리 (Minimun Spanning Tree) (0) | 2023.07.14 |
| A* algorithm (0) | 2023.07.07 |
| Topological Sort (위상 정렬) (0) | 2023.06.29 |



